- 联系人:董先生
- 联系电话:137-10902965
洁净室检测采样方法中的随机抽样理论
若不是ISO 14644-1:1999洁净室及相关受控环境国际标准第一部分“空气洁净度等级”早已过了5 年的应用期,到了重新审核的期限,这个争论恐怕也不会爆发。
ISO/TC209 是负责制订“洁净室及相关受控环境”系列国际标准的技术委员会,其在国际标准化组织 ISO 技术委员会的编号是209。其第一工作组负责 ISO 14644-1 的起草及审核。笔者作为第一工作组的成员,全程参与了对该标准修改的讨论。
1 现有标准在理论上和实际执行中的问题
1.1 现有标准在理论上的问题
在修改讨论之初,本人曾向第一工作组组长、英国标准化学会代表高登先生表达了这样的意见,2~9 个采样点的置信度计算繁复,令人莫明其妙。能否找到较为简单明了、便于采用的方法代替之?不知这一要求是否得到高登的赞同,但他找来一名英国统计学家对现有采样方法中的统计学应用问题进行了全面评估,并向第一工作组全体成员讲述了他的研究结果,介绍如下。
首先,现行标准(ISO 14644-1)对不同面积洁净室适用的是不同的置信度。虽然该标准仅对采样点数量为2~9个的洁净室明确了95%置信度的计算,但我们仍能从采样点数量倒推出对某个面积的洁净室所用的置信度是多少。例如,面积为100 m2的洁净室,采样点数量为 10(即采样点数量 =![]()
其次,若采样点数量为5~9 个时,如果各采样点的粒子浓度均达标,其平均数亦达标的置信度已达到 95%。此时再计算 95%的置信度纯属多余。而当采样点数量为2~3个时,每个采样点达标,但95% 置信度不达标的概率较高。具体而言,2 个点时不达标率为50%,3 个点时也有7%。到 4 个采样点时,每个点达标且平均数也达标,置信度已接近 95%(93.8%)。这里对置信度计算是紧紧围绕着各采样点粒子浓度的平均值进行的,其实质上就是要求对2~9个采样点的洁净室,除每个采样点的粒子浓度要达标外,其各点粒子浓度平均值也要达标。只有这样,该洁净室的洁净度才算达标。
1.2 现行标准实际应用中的问题
现行标准的采样方法不容许在洁净室中有“特别洁净”的地方。如果在采样点中有1~2个采样点的粒子浓度相当低,反而会使洁净室的洁净度不达标。为简单起见,我们以采样点数量为4个的洁净室为例。当4个采样点的0.3 μm粒子浓度分别为950 颗 /m3、950 颗/m3、250 颗 /m3、200 颗 /m3时,其各点均达到 ISO4 级的洁净度等级。但若计算 95% 的置信度,该洁净室等级未达标。原因是其95%的置信度计算结果,超过了每平方米0.3 μm粒子浓度 1020 颗 /m3这个 ISO 4 级的限值。
该标准的制订者一定是预见到了这种情况,于是增加了一条:因异常低的浓度值造成95%置信度计算不达标时,可以去掉这个浓度值,但只能去掉 1 个,并且至少还要保留有 3 个浓度值。这样问题就来了。
(1)对只有 3 个采样点的洁净室,即使有一个采样点浓度异常低,使 95% 置信度不达标,也不能去掉它。否则保留的采样点达不到标准所要求的最低 3 个的数量。按标准要求,该洁净室的洁净度只能以不达标计。
(2)当采样浓度值异常低的点不止一个时,即使去掉一个后,95% 置信度计算仍可能无法达标。上面提到的 950 颗 /m3、950 颗/m3、250颗 /m3、200 颗 /m3的 4 个采样浓度值,若去掉最低的 200 颗 /m3后,以剩余的 3 个浓度来计算 95%置信度,结果仍不达标。
总而言之,现行采样方法显现两大不足:一是未能对各种面积的洁净室一视同仁,它对不同面积的洁净室适用的是不同的置信度,二是不容忍在洁净室中有洁净度异常好的位置。而就是这样一个采样方法,依然沿用了十几年。其制订者的核心思想是,洁净室内粒子浓度是呈正态、大致均匀分布的。
正态分布的意思是,洁净室各处的粒子浓度都应处在浓度“平均值”所允许的偏差范围内。超出这个范围,它就超出了正态分布所允许的范围,也就是由于浓度值异常低,可能是不达标的。
正是基于这个前提条件,标准制订者提出了采样点在洁净室内均匀分布的采样模式,以尽可能覆盖室内各种的情况。并变相地以平均值(95%置信度是在各采样点粒子浓度平均值的基础上再增加一些变换而计算出来的)作为衡量室内粒子浓度是否达标的因素。所以,现行标准的采样方法,至少对2~9个采样点而言是考虑了各采样点粒子浓度值及其相对于平均值的分布范围这两个因素。问题是:考虑洁净室内粒子浓度的平均值,并将此因素纳入对洁净度是否达标的评判,有多大的意义?
2 讨论中的新采样方法
2.1 首先,新采样方法对各种面积的洁净室采取了
一视同仁的置信度,即对应于各种洁净室面积的采样点数量背后的采样置信度是一样的。这个置信度就是 95%,其含义就是以95% 的置信度保证洁净室内至少90% 的面积上的粒子浓度是达标的(见表1)。
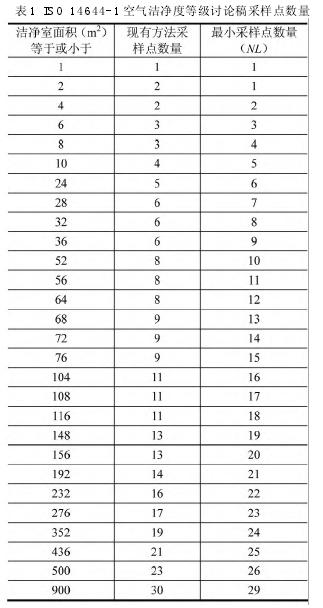
新方法以表格显示出各种面积洁净室对应的采样点数量,清楚、直观、使用方便。且无论采样点数量是多少,均无需再计算置信度。从表中可以看出,与旧方法相比,新方法的采样点数量从洁净室面积为8 m2时开始增加,到500m2时,双方再次接近。其中从大于60 m2到约 300m2时,双方差距最大,新方法比旧方法的采样点数量约多了 50%。新方法在置信度上以及最小保证达标面积比率上,都较旧方法胜过一筹。这也意味着采样工作量的加大,但结果更可靠。
2.2 以置信度计算出采样点数量说明,洁净室空气洁净度分级检测的采样方法是建立在概率论基础上的,即按一定的置信度以有限数量的样本反映整体或一定比例(如 90%)整体的特征。但样本的随机性是这一方法的灵魂。就是说整体中所有样本被抽取受到检测的机会均等,抽到哪一个只是随机而定。无论样本好坏如何,它们都有被测到的同等机会。以此保证抽样的客观性及对整体反映的可靠度。为将此理论应用于洁净室检测,先要以某个单位面积(例如 4 m2)为基本单元,将洁净室划分为若干或更多的等面积单元。按照洁净室的面积找到表1中对应于该面积的采样点数量,从数量众多的等面积单元中,随机选取该数量的单元进行检测。具体检测位置也是在该单元之内随机选定。以 100 m2洁净室为例,它可分为25 个单元,每个单元 4 m2。查表 1 得知 100 m2的采样点数量为 16 个,再在这25 个单元中随机选取16 个进行采样。见图 1。

这个随机选点过程不是由人随意选定的,是根据随机数字发生器产生的随机数字,选定编号相同的单元确定的。
这一方法的随机性是最佳的,每次抽样时尚未被抽到的单元被抽到的概率是完全相等的。所以,被抽到的单元不会均匀或大致均匀分布在洁净室中。采用这种抽样方法可能在洁净室中留下大片未抽到区域,同时,有些采样点会显得相对集中。洁净室面积越大,这种趋势越明显。
那么这种方法能够反映洁净室粒子浓度的全貌吗?问题还要从对4 m2的单元分析开始。按随机抽样理论,每个样本性质相同,各自独立,互不影响。例如对产品质量的抽检,每件产品都是以基本相同的原材料,同样的机器,同样的工艺,甚至相同的工人操作而生产出来的。它们总的内在质量应该是基本一致的。这时用随机抽样方法进行检测,找出可能混
杂于其中的不合格产品,是一种省时省力的方法。
但处在洁净室中的这 4 m2空间,每个 4 m2的空间可能各不相同,如处在风口之下的、风口之间的,或在无风口处的,它们情况也是各有不同。而且由于这个小单元并未“与世隔绝”,也只有在空态的垂直层流洁净室内,这4 m2的单元可能处于“最理想”的状态。即特性大体一致,各种独立,互无干扰和影响。混合流洁净室无论处于三种占用状态的哪一种,或对处于静态或动态的垂直层流洁净室,其基本单元的统一性和独立性都是要大打折扣的。
既然随机抽样的前提条件不那么“纯粹”,既然这种随机采样方法可能不能反映洁净室粒子浓度分布的全貌时,我们能否将其“改良”一下呢?这就是所谓的“半随机”采样。
它就是按表1中所列的洁净室采样数量,将该洁净室分割为均匀的等面积块,再在每块之内任意选取采样点实施采样。还是以100 m2的洁净室为例。按表1所列的100 m2洁净室的最小采样点数量是16个。将这100 m2划分为16个等面积区域。再在每块中任意选择具代表性的采样点位置进行采样。见图 2 所示。

按这种采样方法,每个位置均有被采到的机会,但被采到的机会都是只有1次。它克服了现行方法只在每块区域中央采样的机械性,同时又照顾到采样点分布的大致均匀性。避免采样点过偏或集中的情况发生。由于这个方法还是具有一定的随机性,它在原则上仍保留有随机性的成分。
3 结论
“全随机”采样方法更符合随机抽样理论的要求和条件,而“半随机”采样方法还考虑到了洁净室内在各种情况下不同位置所具有的不同特点。“半随机”采样方法承袭了现有将洁净室分成等面积采样区的方式,又不拘泥于以采样区中心点为采样位置的“机械性”。现有方法已在国际上通行了十几年,新方法也考虑到其传承性。
医院空气净化管理规范WS/T368-2012
回风口的设置对高等级级洁净层流手术室的影响
无线监测洁净厂房温湿度控制系统
如何计算医院诊室的新风量
工业洁净车间冷热源选择
工业洁净车间空调净化系统节能改造实例
通过 LCD 洁净间气流改善提升良品率
竖井型城市隧道火灾烟气流动模拟分析
上一条:洁净室空调系统竣工现场调试参考下一条:洁净室消毒臭氧量如何计算?


